¿Cómo se puede utilizar el crochet para modelar la nanociencia?

Originalmente publicado en inglés
Publicado el 11 de abril del 2024
Traducido por Regina González Lona,
Editado por Wilanyi R. Alvarez Reyes y Lissett G. Diaz

¿Qué tienen que ver las nanopartículas de plata con los copos de nieve y el crochet? Por lo general, ¡no mucho! Pero recientemente, los científicos han creado métodos para hacer formas parecidas a copos de nieve a partir de nanopartículas de plata,¹ y sus métodos me recordaron no sólo a los copos de nieve sino también a cómo hago algunos de mis propios proyectos de tejer.

izquierda: nanocristal gris oscuro con forma de copo de nieve (barra de escala 500 nm). Derecha: forma de copo de nieve tejido a crochet de color gris claro con 12 brazos ondulados (barra de escala de 2 cm) — Izquierda: un cristal a nanoescala de nanopartículas de plata recubiertas (imagen utilizada con autorización de Ratout et al. 2022, ACS Nano¹). Derecha: un copo de nieve tejido a crochet (foto de Abby Stitgen, patrón cortesía de Irarott.com ⁴).

Entonces, ¿qué tienen en común estas diferentes formas? Los copos de nieve, como muchas otras estructuras del mundo natural, están compuestos de patrones llamados fractales. Los fractales son formas complejas que tienen unidades que se repiten a sí mismas, lo que significa que no importa cuán alejado o cercano estés, la forma parecerá consistente.

Tomemos, por ejemplo, un árbol desnudo. Al alejarlo, puedes ver un laberinto de diferentes ramas que salen de un tronco principal para formar todo el árbol. Si te acercas a una rama, comenzará a parecerse a un tronco del que salen ramas más pequeñas. Y si nos acercamos más, las ramas más pequeñas tienen aún más ramitas saliendo de ellas. Cada vez que hace zoom, la imagen consta de una unidad de repetición similar. Aunque eventualmente la rama de un árbol terminará en un capullo de hoja o una flor, en un fractal matemático puedes seguir acercándote infinitamente.

Izquierda: fotografía en blanco y negro de un árbol sin hojas con muchas ramas pequeñas. Derecha: dibujo lineal en forma de árbol que comienza con una sola línea en la base que se bifurca en una Y, con cada rama de la Y bifurcándose en dos, y cada una de esas ramas bifurcándose en dos, repetida una y otra vez. — Izquierda: Ilustración de cómo los árboles naturales tienen patrones de ramificación repetidos, lo que los convierte en un fractal natural (Imagen de Mila Tovar). Derecha: un “árbol” fractal creado al hacer que cada línea se ramifique en exactamente dos nuevas ramas (imagen de Saisundar.s).

¡Los patrones fractales también entran en juego con los copos de nieve! En los copos de nieve, los cristales de hielo se forman como capas de moléculas de agua que se adhieren a las superficies congeladas del copo, y las esquinas se acumulan más rápido que los bordes formando un hermoso patrón de seis lados (consulte “La ciencia de la nieve” para conocer más detalles). Esto también crea un fractal natural, con los brazos teniendo regiones de ramificación adicionales que crean una sensación de autosemejanza independientemente de qué tan cerca estés del copo de nieve.

Micrografía azul y blanca de un copo de nieve cristalino — *Ejemplo de un copo de nieve donde cada sección tiene cristales fractales que se ramifican (imagen de Libbrecht 2005²)*

Pero, ¿qué pasa con el crochet? Como una entusiasta artista de fibras, también me alegra saber que los fractales sirven para crear patrones fáciles de tejer. Esto me ayudó a visualizar realmente cómo funciona el acercamiento y alejamiento de fractales simplemente relacionándolo con un proyecto parcialmente terminado. Tome este tapete que creé para comprender un poco mejor los fractales:

hilo morado tejido a crochet en forma de espiral

En las primeras etapas de la creación del diseño, forma un patrón en espiral distintivo.

Fotografías una al lado de la otra del mismo hilo morado que en la foto anterior, que muestran etapas progresivamente más grandes del proyecto con un patrón en espiral creciente.

A medida que lo construí más, se mantuvo de la misma forma general. No importaba qué tan avanzado estuviera el patrón, todavía se veía muy similar, solo que en un tamaño diferente.

el mismo proyecto de crochet en espiral morado que muestra un mayor progreso con una capa azul alrededor del exterior

Ésta es una de las características clave de un patrón fractal: es autosemejante a diferentes aumentos.

Proyecto de tapete de crochet terminado que muestra el patrón en espiral que comprende púrpura en el centro, rodeado por una capa azul oscuro y una capa azul claro alrededor del exterior.

Un patrón fractal de ganchillo. Independientemente de qué tan ampliado o qué tan “hecho” esté el patrón, la forma general de la espiral sigue siendo muy similar. Los diferentes colores no son intencionales porque me quedé sin hilo. Observe el mismo ganchillo rosa en cada foto para tener una idea del tamaño creciente. (Fotos cortesía de Abby Stitgen, patrón cortesía de Zouzou Crochet ³.)

En el mundo natural, así como en el crochet, existen límites en cuanto a qué tan pequeño o grande es el objeto antes de que deje de repetirse. Tomemos, por ejemplo, un copo de nieve tejido a crochet. En el patrón que hice, hay doce brazos que se extienden desde el centro alternando brazos largos y cortos, y en cada uno de esos brazos hay más perillas ramificadas (llamadas “picots” en términos de crochet). Sin embargo, es prácticamente imposible agregar más ramas al diseño (al menos, usando el mismo hilo) debido a los límites de lo pequeño que es un solo punto.

izquierda: copo de nieve tejido a crochet de 12 brazos de color gris claro. Derecha: vista ampliada de dos brazos que muestran los puntos ondulados — El copo de nieve de crochet se forma agregando bucles repetidos a cada capa que se extiende desde el centro. En cierto punto, es imposible continuar con el patrón de ramificación (foto de Abby Stitgen, patrón cortesía de Irarott.com ⁴).

Esto es cierto para todos los fractales naturales: las ramas de los árboles eventualmente terminan, los copos de nieve no pueden seguir acumulando hielo más allá de un diámetro pequeño y una rama de crochet no puede ser más pequeña que una sola puntada. Pero en teoría, los fractales pueden repetirse un número infinito de veces. Tomemos, por ejemplo, una forma geométrica llamada copo de nieve de Koch:

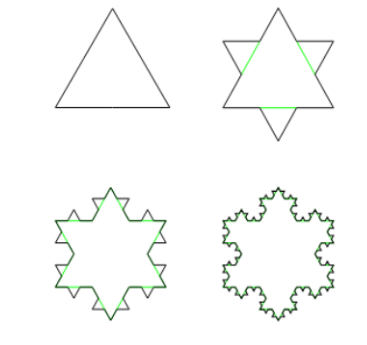
arriba a la izquierda: un triángulo simple. Arriba a la derecha: cada lado del triángulo simple tiene un triángulo más pequeño que sobresale para formar una estrella de seis lados. Abajo a la izquierda: cada lado de cada triángulo más pequeño tiene otro triángulo más pequeño que sobresale del medio, por lo que la forma general comienza a parecerse a un copo de nieve. Abajo a la derecha: cada lado de cada triángulo de tercer nivel tiene otro triángulo que sobresale, formando en general una forma detallada de copo de nieve. — *Los primeros pasos para construir un copo de nieve de Koch agregando más y más triángulos (imagen de Chas zzz brown & Shibboleth).*

En este diseño, cada iteración agrega un nuevo triángulo equilátero en el lado externo de un triángulo anterior. A medida que se va construyendo, la estructura adquiere la forma de un copo de nieve. Acercar cualquier lado externo, sin importar cuánto lo haga, daría la misma imagen de un triángulo con triángulos cada vez más pequeños adjuntos, repitiéndose hasta llegar a un triángulo infinitamente pequeño.

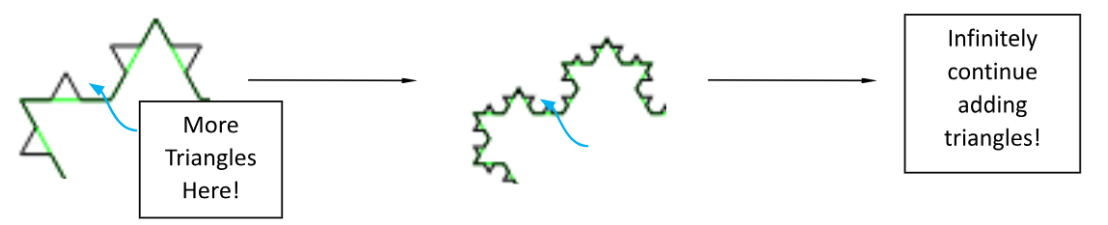
izquierda: amplíe la parte inferior izquierda de la figura anterior, etiquetada "más triángulos aquí" con una flecha que apunta a un triángulo más pequeño. Derecha: amplíe la parte inferior derecha de la figura anterior, con una flecha hacia la derecha etiquetada "¡Continúe agregando triángulos infinitamente!" — *El copo de nieve de Koch se forma añadiendo nuevos triángulos a cada cara de un triángulo existente; (diagrama de Wikipedia).*

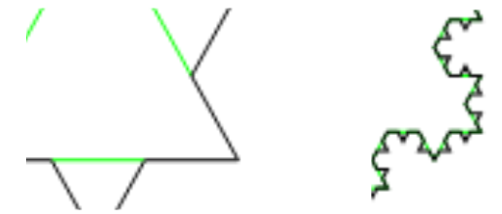
Ahora, volvamos a la nanotecnología. Recientemente, se ha investigado mucho sobre formas de aplicar diseños fractales a diferentes tecnologías. Después de todo, la previsibilidad de la estructura y la gran superficie pueden crear propiedades muy deseables que ya han sido explotadas en organismos naturales como árboles y plantas. Hemos hablado mucho en este blog sobre cómo el aumento de la superficie es un aspecto muy importante de la nanotecnología, y puedes ver que la superficie de la derecha es mucho mayor que la de la izquierda:

izquierda: ampliación de parte de una estrella simple de seis caras. Derecha: ampliación de parte del triángulo de Koch de cuarto nivel, compuesto por muchos triángulos pequeños — *La superficie “más irregular” del fractal de la derecha tiene más superficie que la superficie lisa de la izquierda. (diagrama de Wikipedia)*

En un ejemplo del uso de fractales en nanociencia, los científicos han podido diseñar un fractal parecido a un copo de nieve hecho de nanopartículas de plata. Utilizaron péptidos para unir las nanopartículas de plata, haciendo que se agregaran en estructuras fractales hiper ramificadas.

Izquierda: nanocristal gris oscuro con forma de copo de nieve (barra de escala 500 nm). Derecha: vista ampliada de parte de una rama, que muestra pequeñas extensiones que se ramifican en los extremos (barra de escala de 100 nm) — *Un ejemplo de nanopartículas de plata recubiertas que forman un patrón fractal similar a un copo de nieve. (Imagen utilizada con autorización de Retout et al. 2022,* ACS Nano¹)

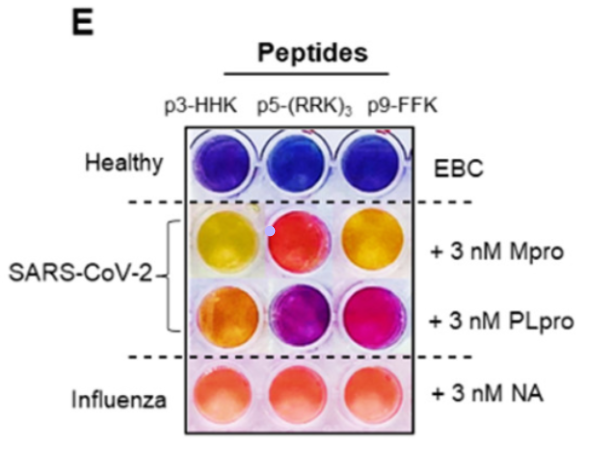
Estudios preliminares han descubierto que estos fractales de nanopartículas de plata pueden usarse como sensor colorimétrico para diferenciar virus. Brevemente, lo que esto significa es que cuando se añaden proteínas virales a los péptidos puente y a las nanopartículas de plata, las proteínas virales pueden interferir con la construcción de los fractales de plata. Todo esto se puede visualizar a simple vista, donde las soluciones fractales son de un azul intenso y las soluciones con interferencia de virus son más rojas y amarillas. Aún más impresionante, los investigadores que realizaron el estudio pudieron diferenciar (¡con 100% de precisión!) entre muestras enriquecidas con coronavirus y muestras enriquecidas con influenza completamente por esta diferencia de color de interferencia fractal.

Conjunto de círculos de colores de tres a lo ancho y cuatro hacia abajo, con diferentes péptidos etiquetados en la parte superior y una interpretación a lo largo de los lados. La fila superior es de color azul violeta y está etiquetada como Saludable. Las dos filas del medio son de color amarillo a violeta claro y están etiquetadas como SARS-CoV-2. La fila inferior es naranja y está etiquetada como influenza. — Un ensayo colorimétrico utilizado para distinguir muestras sanas de muestras enriquecidas con proteínas de coronavirus (Mpro y PLpro) y muestras enriquecidas con proteínas de influenza (NA). (Imagen utilizada con autorización de Retout et al. 2022, ACS Nano¹)

A medida que los científicos continúan descubriendo nuevas formas de crear fractales a nanoescala, podemos seguir aprovechando sus propiedades únicas. Otros beneficios de sus altas áreas superficiales pueden incluir la mejora de la actividad catalítica, y las propiedades ópticas mejoradas pueden explotarse en nuevos sensores. Los fractales demuestran que las formas naturales comunes pueden ser bastante geniales y tener propiedades científicas asombrosas.

Referencias

Retout, Yash Mantri, Zhicheng Jin, Jiajing Zhou, Grégoire Noël, Brian Donovan, Wonjun Yim, and Jesse V. Jokerst. ACS Nano 2022 16 (4), 6165-6175 DOI: 10.1021/acsnano.1c11643
Libbrecht, K. The physics of snow crystals.Reports on Progress in Physics, 2005, 68 (4), 855-895. doi: 10.1088/0034-4885/68/4/R03
Doily crochet pattern: https://zouzoucrochet.com/spiral-star-doily-free-crochet-pattern/
Snowflake crochet pattern: https://irarott.com/blogs/free-patterns/christmas-snowflakes-crochet-pattern